Um modelo cinemático é uma representação matemática do movimento de um robô que se concentra nas relações geométricas entre elementos e ignora forças externas que afetam o movimento. Modelos cinemáticos são usados para planejar e controlar os caminhos dos robôs industriais.
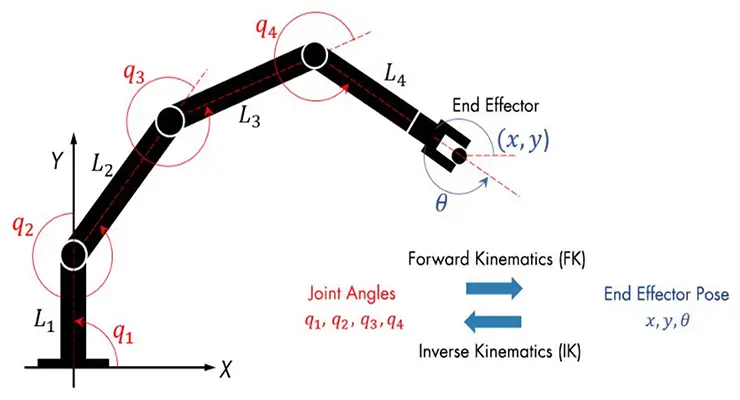
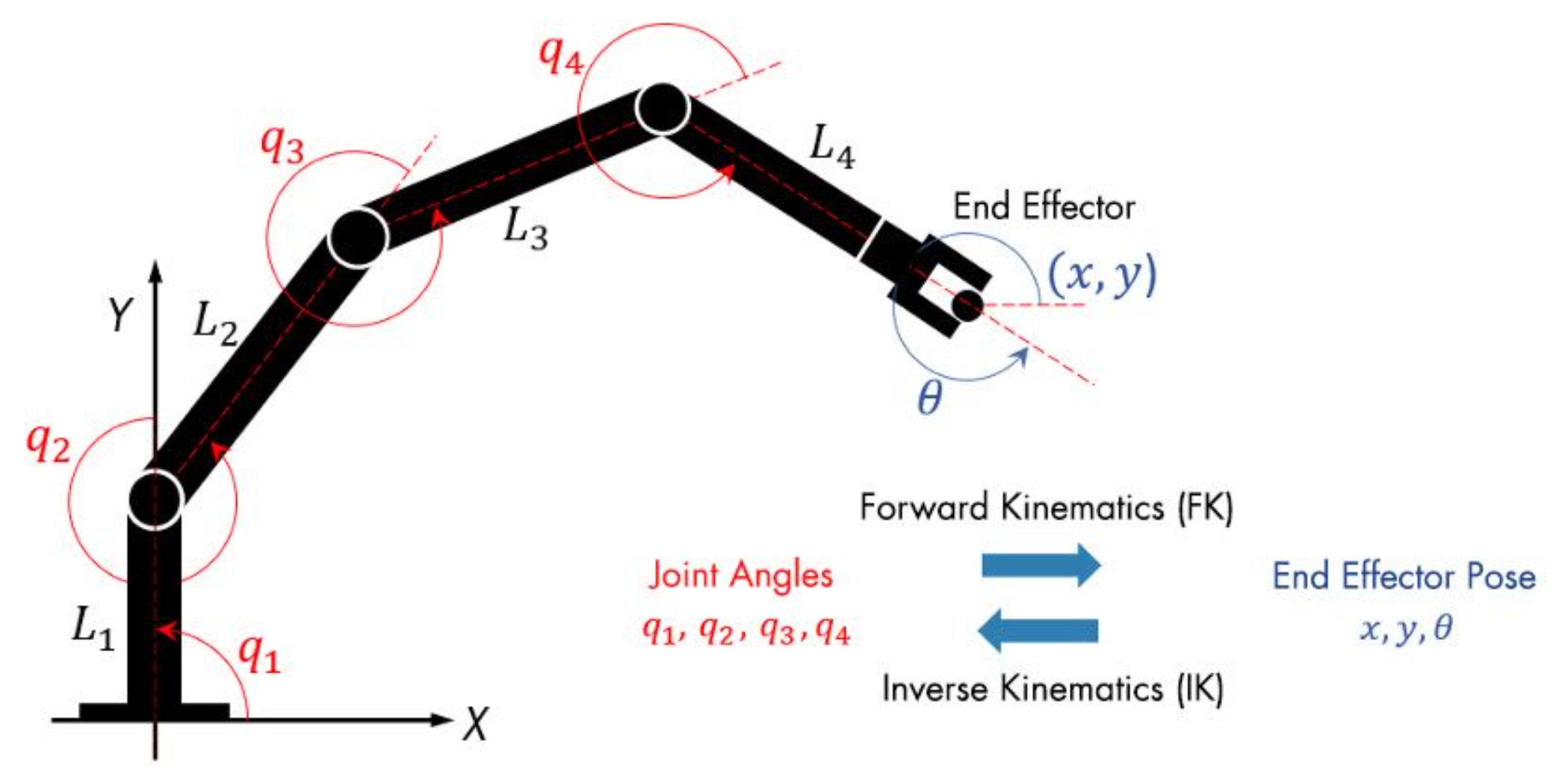
A cinemática direta determina a posição e orientação atual do efetor final com base nos ângulos de cada articulação no braço do robô. Os cálculos usam uma série de matrizes de transformação contendo ângulos de articulação, comprimento e parâmetros de deslocamento.
As matrizes de transformação são multiplicadas sequencialmente da base do robô para o efetor final. O resultado é a posição nas coordenadas tridimensionais e na orientação do efetor final (em termos de ângulos). A cinemática inversa reverte o processo, determinando os ângulos articulares necessários com base na posição do efetor final, como mostrado em Figura 1.
Convenção de Denavit-Hartenberg
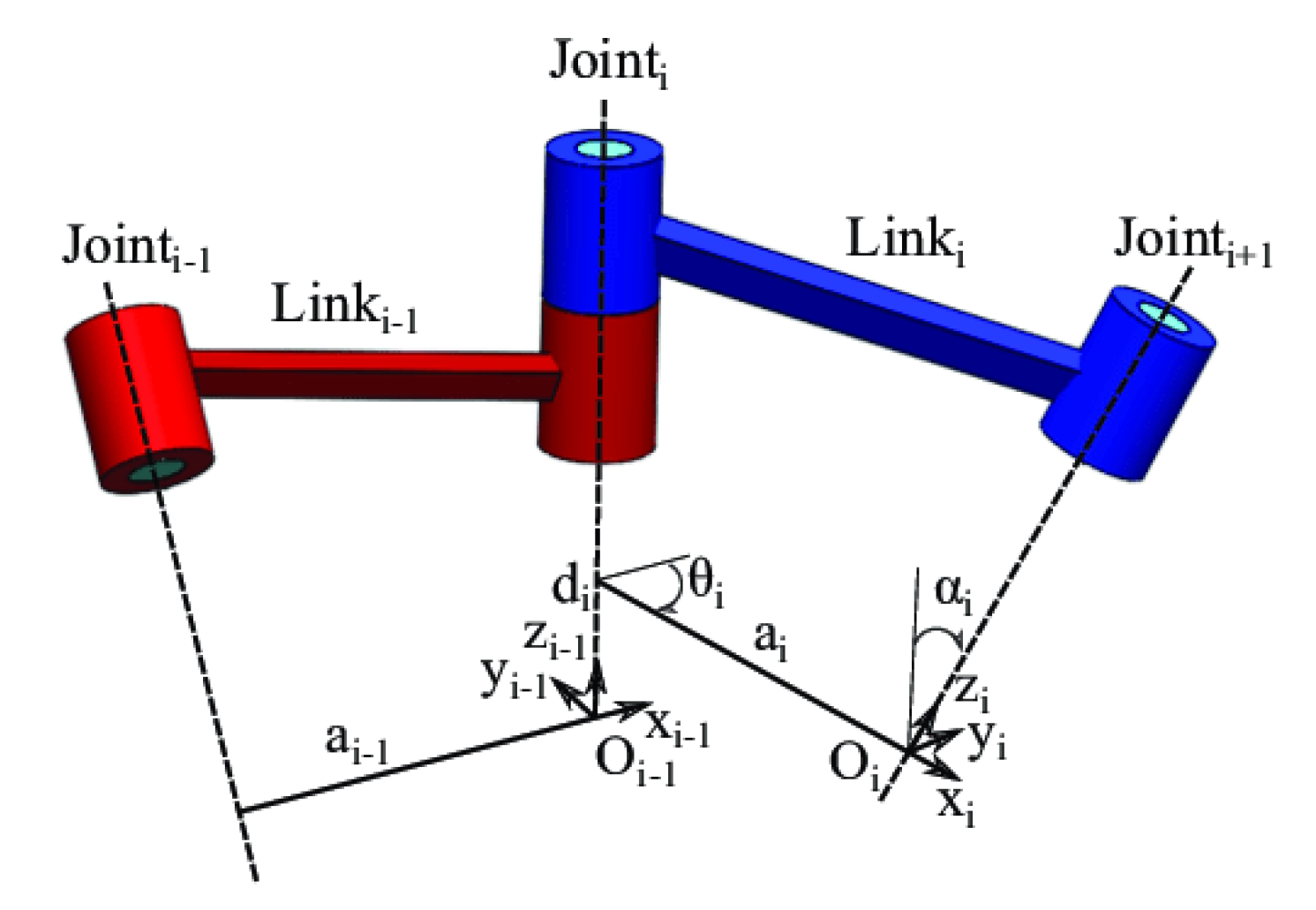
A Convenção de Denavit-Hartenberg (DH) é uma maneira padronizada de representar a geometria e os ângulos articulares de um robô. Ele detalha como anexar quadros de coordenadas às juntas em um robô, definindo a posição relativa e a orientação entre as juntas adjacentes.
Cada articulação, ou link, é descrita por quatro parâmetros, incluindo o comprimento do link (a), ângulo da articulação (θ), deslocamento de link (d) e torção articular (α), como visto em Figura 2. Os quatro parâmetros são usados para calcular matrizes de transformação para cada articulação. As matrizes podem ser multiplicadas para determinar a transformação geral da base de um robô para o efeito final. Os sistemas de controle usam os parâmetros DH para calcular os ângulos da junta necessários para alcançar poses desejadas do efetor final.
Matriz jacobiana
A Convenção DH pode ser usada juntamente com matrizes jacobianas para relacionar velocidades das articulações com as velocidades do efetor final. As velocidades das articulações podem descrever a rapidez com que a articulação está girando para uma articulação de revolução e a rapidez com que a articulação está se estendendo ou se contraindo para uma articulação prismática.
A matriz jacobiana (J) é uma matriz de derivados parciais que descreve a relação entre as velocidades articulares e a velocidade do efetor final. Em sistemas de controle de robôs, J é usado para mapear as velocidades da junta para a velocidade do efetor final.
Transpondo J Permite o cálculo dos torques da junta necessários para produzir forças desejadas no efeito final. Em planejamento de movimento, J é usado para identificar e evitar singularidades, onde o robô perde a capacidade de se mover de forma livre e precisamente. Uma singularidade ocorre quando o determinante de J torna -se zero.
Singularidades
Em uma singularidade, a relação matemática entre ângulos articulares e a posição do efetor final quebra, e o robô perde um ou mais graus de liberdade. Singularidades ocorrem quando várias articulações se alinham de uma maneira que impeça que o robô se mova em uma ou mais direções. Isso pode resultar em perda de controle, instabilidade ou movimento espumoso. As configurações de singularidade podem ser evitadas com um projeto cuidadoso de trajetórias de movimento.
Manipulabilidade
Singularidades são uma forma de manipulabilidade limitada. A manipulabilidade mede o quão bem o robô pode alterar a posição do efetor final com base na configuração conjunta atual. A manipulabilidade é medida usando a decomposição de valor singular de J Para calcular o elipsóide de manipulabilidade.
O elipsóide de manipulabilidade representa visualmente a capacidade do robô de se mover em diferentes direções. Um elipsóide com um volume maior indica maior manipulabilidade. Uma proporção do eixo elipsóide próximo a 1 indica manipulabilidade igual em todas as direções, conhecida como manipulabilidade isotrópica. Uma grande proporção sugere que uma singularidade está se aproximando.
Resumo
As equações cinemáticas são usadas para determinar a trajetória ideal para passar de uma pose para outra e para evitar dificuldades como singularidades que podem limitar o movimento de um robô. A Convenção DH é uma maneira padronizada de representar a geometria e os ângulos articulares de um robô. A matriz jacobiana fornece uma estrutura computacional para otimizar os movimentos do robô.
Referências
Como calcular a cinemática de um robô em 5 etapas fáceis. Robotiq
Introdução a robôs autônomosfivável
Equações da cinemáticaWikipedia
Modelo cinemáticoScienceDirect
Parâmetro cinemática Calibração de robôs industriais em série com base na medição de pose parcialMDPI Mathematics
Planejamento de trajetória ideal multi-objetiva para braços robóticos usando profundo aprendizado de reforçoSensores mdpi
Cinemática do robôMel
O Guia final de matrizes jacobianas para robóticaAddison automático
Eeworld Online Related Content
Como os robôs podem melhorar a experiência de sorvete?
Quais são as principais especificações dos sensores de visão de máquina?
Quais são os tipos e usos dos sensores de posição?
Qual é o papel da fusão do sensor na robótica?
Padrões internacionais de desempenho e segurança para robôs